At some point, if you have talked about fractions in general conversation with your child from an early age (see Fractions for four-year-olds), he may ask you how you write fractions. Or he may see fractional notation in a book, and want to know what it means.
Writing fractions
Although many people find fractions confusing, the basic notation is quite logical: for instance, the fraction ‘half’ means one item divided into two pieces (or shared between two people). We use a line, either a horizontal one or a slash, to show this, so ‘half’ is written 1/2 or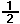 
.
Similarly a ‘quarter’ (known as ‘fourth’ in some countries) means one thing divided into four pieces, and is written 1/4 or 
.
To start with, this may be sufficient new notation for your child – he may want to play around with writing fractions like this, and there’s no need to move on until he’s ready. When he asks more, you could try out various other simple fractions and illustrate them, with circles or squares divided into different numbers of sections. For instance a graphic representation of a quarter could be:
But what happens when you want more than a simple sharing? For instance, if you want not one quarter of an object, but three-quarters? This is easy to draw:
and the way of writing it equally logical: 3/4 or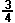 
. It’s worth pointing out, if your child understands simple multiplication (if not, see beginning multiplication) that this is a short-hand way of writing 3 lots of one quarter, or
3 x .
If you have a pie cut into four quarters, and three people each eat a slice, then three quarters are gone.
Thinking about what fractions mean
Ask your child what he thinks four quarters would be. Some will immediately ‘see’ that this is the same as one whole item, particularly with a picture in front if them, and others will try writing something like 4/4. This is not wrong – never discourage your child when he is thinking about how something works. Four quarters is indeed logically written 4/4. Tell your child that he’s right, and that another way of thinking of it is the whole thing.
This may be obvious to you, but many children find it quite a complex concept, so spend some time – perhaps over several days or weeks – pointing out casually how this works in everyday terms. For instance if you have a pie, and cut it into four equal pieces, each piece is one quarter. But the pie is still all there, even though it is now divided into four quarters. If four people each have one of the pieces, then the whole pie is gone.
Repeat this practical example when you divide something into half, or thirds, or fifths, until it becomes obvious to your child that there are lots of different ways of thinking of the number one: two halves, or three thirds, or five fifths, and so on. If your child likes thinking about large numbers, try asking what fifty-seven fifth-sevenths would be, or a hundred hundredths, or a billion billionths…! However if your child is still thinking in concrete terms and cannot yet comprehend large numbers, leave this for a while.
Once your child fully understands simple fractions, you can begin to explain how to add fractions of the same order. Indeed, he may have realised it already. Think back to the pie where three-quarters was eaten. What remains? Obviously one quarter. Three-quarters plus one quarter makes four quarters – which, of course, is the same as one whole item. What about three-fifths plus one-fifths? Try this with a real pie or cake, or draw a diagram like this:
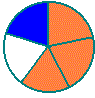
From this it’s clear that three-fifths plus one-fifth makes four-fifths. Or, to write it in fractional notation:
Another one-fifth would make five-fifths, or one whole:
Thinking about fraction concepts
Your child may quickly grasp the concept that fractions like this can be treated like objects. As three apples plus one apple make four apples, so three fifths plus one fifth makes four fifths. Six tenths plus two tenths will make eight tenths, just as six bananas plus two bananas make eight bananas. If this doesn’t strike your child, or if he finds the idea confusing, try some of the suggestions in my article Algebra for six-year-olds for understanding these concepts more easily.
However, of course, fractions are not the same as objects, so don’t take this analogy too far, particularly if your child sees it quickly without analogy. Unlike apples and bananas, fractions don’t have to be the same ‘sort’ in order to add them up. One quarter plus one quarter makes two quarters, but a quick diagram will show that two quarters is the same as one half:
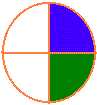
1/4 + 1/4 = 2/4
1/4 + 1/4 = 1/2
2/4 = 1/2
Dividing a cake or pie into two pieces and then cutting each of those in two will demonstrate this easily. Two quarters make a half, and half of a half will be a quarter. So in fact it’s quite easy to add up a half and a quarter, to make three-quarters:
1/2 + 1/4 = 3/4
This can be done because a half is the same as two quarters, and then two quarters added to one quarter makes three quarters:
1/2 + 1/4 = 1/4 + 1/4 + 1/4 = 3/4
An apple cannot so easily be added to a banana!
Don’t necessarily expect your child to understand all this at once. If you try and introduce the topic and he’s clearly bemused, leave it alone entirely for a while, or just mention simple fractions in passing, from time to time, until he wants to know more. Once he grasps the concepts fully, whether he is three or thirteen (or any other age!) he will be able to extend them to more complex fractions without too much difficulty. The worst thing you can do is to try and ‘drill’ him into doing written fraction work before he has fully understood what fractions are, and how they relate to real life.
For more articles about teaching basic maths without workbooks or drill, see:
Beginning multiplication
More complex multiplication
Prime numbers and factors
Algebra for six-year-olds