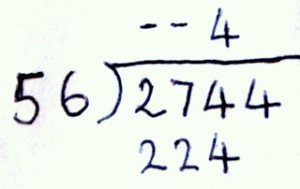Long division is something we probably all learned during our primary or early secondary years, and – in many cases – have entirely forgotten. It’s a complex technique, one which in today’s era of calculators and computers may seem redundant. Nonetheless, there are many who believe that it’s an important technique, part of general knowledge for the majority. If you feel that your home educated students are never going to need it, and have no interest in it, then by all means continue to use a calculator. But if your children are interested in the method, this page might help.
Basic division or sharing
First of all, ensure that your children understand basic division. The concept is one we use in everyday life, and which children as young as five or six usually grasp naturally; but not every child is mathematically inclined, and some may have missed out on the topic. So it’s vital to give at least a quick overview of the principles, using the word ‘sharing’ if you like it better than ‘division’.
Make sure, too, that they have a good grasp of the principles of multiplying, including the multiplication of two-digit numbers. It’s also extremely important to understand the concepts of place value before attempting long division.
What is long division?
Long division refers to any problem of dividing that cannot easily be done in the head, or by cancellation on paper. If you are asked to divide 400 by 20, for instance, you can probably ‘see’ that it’s the same as 40 divided by 2, and that the answer is 20. If you’re asked to divide 369 by 3, then a good grasp of number patterns will enable you to spot that 369 is 300 + 60 + 9, so dividing the whole by 3 will give 100 + 20 + 3, or 123. In daily life, many arithmetic problems of this kind have straightforward answers, and part of good mathematical training is helping children to see which techniques are appropriate for different circumstances.
Long division, then, would refer to the technique of solving a more complex problem such as – for instance – 2744 divided by 56. This would daunt many. You could certainly divide both by 4, to give 686 and 14 and thus reduce it to a simpler sum, but let’s take the original and see how it works.
Layout of long division problems
To start a problem of this kind, it’s usual to write it down something like this:
____
56 ) 2744
There needs to be space below for the working, and space above for the solution.
We work from left to right in long division, taking one digit of the dividend at a time. Can 2 by divided by 56 to give a whole number? Obviously not. So the answer is not in the thousands. Move one space to the right. Can 27 be divided by 56? Again, clearly not as 27 is smaller than 56. It may help to put little dashes above the 2 and the 7 at this stage but it’s not essential.
Now move along one more digit. Can 274 be divided by 56? Yes, it can. So we need to estimate how many times. 50 would go into 274 five times, with a remainder of 24; 60 would go into it 4 times with a remainder of 34. A quick check determines that 56 x 5 = 280 (too much) while 56 x 4 = 224. So the first digit of the answer is 4, and we write 224 down underneath the 274, and get something like this:
Now 224 is subtracted from 274, giving 50 as remainder. This should be written beneath, something like this:
Clearly 50 cannot be divided by 56, so we now ‘bring down’ the final digit, the last 4 of the dividend, and ask how many times 504 can be divided by 56. It turns out that the answer is exactly 9 times. So the answer to the problem is 49. If there were a remainder at this stage – if, for instance, the dividend had been 2746 instead of 2744 – then that would be left as part of the answer, labelled ‘remainder’.
How does long division work?
Long division is not an intuitively obvious process. It can best be understood as a series of multiple subtractions in order to divide. This may be more clearly grasped with a simpler example, such as the one given above: 369 divided by 3. Thinking in terms of a real-life (if unlikely) scenario, let’s say we have 369 tennis balls, and they must be equally shared between three tennis courts.
To do that, we could walk from one court to another, putting one ball in each, until we’ve been to each of them 123 times. That would be a lengthy process; at the end of each round of visits we would have subtracted three more from the total. It would be more efficient to leave, say, ten balls at a time in each court, and see how many times we could do that. This would subtract 30 balls each round, which would be a much quicker process, but we’d eventually get stuck, after 12 rounds, because 30 times 12 is 360, and there would only be 9 balls left.
We would know that each round of 30 balls was like 10 rounds of 3 balls, so the 12 rounds of 30 balls is equivalent to a time-consuming 120 rounds of 3 balls each. And the final 9 can easily be divided into three sets of three, meaning that each court ends up with 123 balls.
The long division method, as shown above, essentially turns this into an algorithm – a technique that enables us to make the best guesses as to how many times we need to subtract a number without too much guesswork.
Practising long division
You can find another worked example, in even more detail, on the mathsisfun site; at the end are some examples to help you practice (pen and paper recommended). Snork’s long division game is an animated way of going through long division, step by step, choosing different levels of complexity. After several examples you may find that the process becomes natural, and may even make sense; equally you may never fully understand it.
It’s important to be able to do long division if you want to do complex algebra; but if your child has no interest in maths, and is educated at home, then in most cases a calculator will solve this kind of problem much more quickly.